En este link tienen acceso a una entrada sobre el uso básico de Solver, aquella poderosa herramienta que Excel nos provee para resolver problemas complejos, en los cuales juegan distintas variables y restricciones. El ejemplo era sencillo, aspecto que hoy cambiaremos, para complicar un poco mas la cosa y aprender mas sobre Solver. Desarrollaremos un ejercicio con ciertos aspectos mas complicados, para que todos aquellos que desconocen sobre Solver lo empiecen a tener en cuenta en sus proyectos.
Repito lo dicho: una de las principales cuestiones pasa por plantear correctamente el problema, identificar las variables y restricciones y, por último, llevar todo eso de forma conveniente a una planilla.
Aclaración: puede resultar un poco "duro" digerir este ejemplo (quizás), pero no se desanimen: se bajan el archivo de ejemplo y mientras leen el post lo van analizando; el resultado final vale cada segundo invertido.
[+/-] Ver el resto / OcultarAclaración: puede resultar un poco "duro" digerir este ejemplo (quizás), pero no se desanimen: se bajan el archivo de ejemplo y mientras leen el post lo van analizando; el resultado final vale cada segundo invertido.
Empecemos: somos propietarios de 4 plantas que fabrican memoria Ram, las cuales se encuentran distribuidas a lo largo y ancho del país. Cada planta tiene una capacidad determinada de producción:
queda claro: tengo una producción mensual de 300 unidades de memoria Ram, entre las 4 plantas
Esta producción no queda en las plantas, si no que debe ser enviada a 4 ciudades del país, en donde poseemos depósitos de distintas capacidades. El tamaño de los galpones es un tema a tener en cuenta, ya que difieren y no puedo almacenar la misma cantidad de memorias en cada uno. Veamos en el siguiente cuadro la capacidad de los depósitos:
bien: tenemos en total 300 lugares disponibles de almacenamiento, repartidos en distintas ciudades.
Resumiendo: produzco 300 unidades y tengo que llevarlas hasta los depósitos situados en las ciudades de Rosario, Córdoba, Mendoza y Salta. Cada ciudad tiene una capacidad limitada de almacenamiento distinta ¿Todo bien hasta acá?. Sigamos.
Transportar la mercadería (en camiones, trenes, aviones, carretas o barcos) conlleva un costo determinado, el cual traduzco en la siguiente tabla:
breve y sencillo: llevar mercadería desde la planta 1 a Mendoza me cuesta $300, de la planta 3 a Rosario $700, de la planta 4 a Salta $800 y así sucesivamente. Cada cruce de fila/columna nos indica el costo
Teniendo en cuenta los valores arriba indicados, mas nuestra producción y la capacidad almacenamiento en cada depósito....¿Como hacemos para que Solver nos diga la forma mas barata de distribuir las 300 memorias Ram? Porque mover la producción conlleva un costo: no es lo mismo enviar desde la planta 3 a Rosario ($700) que enviarlo a Córdoba ($1300), la segunda opción es mucho mas económica. Pero hay varias plantas y ciudades en juego ¿como determinamos lo que nos resulte mas ecómico y, a la vez, mas rentable a nuestro negocio?
Armo una pequeña tabla, a la cual completaré primero manualmente para que se entienda bien el propósito de este ejercicio:
Explicación: aquí diseñé un pequeño modelo de gasto. El total de producción de la planta 1 lo envío a Rosario y Mendoza, el de la planta 2 a Rosario, Córdoba y Salta, el de la planta 3 a Mendoza y Salta y, por último, lo producido en la planta 4 lo remito a Rosario, Mendoza y Salta. Es sólo un ejemplo, algo que hice "a mano" para ir probando cuanto me cuesta el desplazamiento de la mercadería. ¿Cuanto? $256.000.
Siguiendo con la misma temática, ya que quiero encontrar algo bien barato, exploro otras opciones:
Con esta nueva configuración ahorré $6.000. Toda la producción de la planta 1 la envié a Mendoza, el total de la 2 a Rosario, el total de la 3 a Salta y de lo producido por la planta 4, 50 memorias a Córdoba y 10 a Salta. Liberé toda la producción y colmé los depósito (idem a la tabla anterior), con la salvedad de que en este caso me salió $6.000 mas barato. ¿Hasta cuando puedo probar manualmente, combinando las distintas posibilidades, y estar fehacientemente documentado de que estoy optando por el método de distribución mas económico? ¿Por que no dejo el papel y la birome y llamo a Solver para que me ayude?
Antes de llamar a Solver aclaremos como llegué a cada valor total (256000 y 250000): lo hice utilizado dos tablas: la de los precios y la de cantidad de memorias enviadas, utilizando la función =SUMAPRODUCTO(matriz1, matriz2) para multiplicar los costos de cada envío:
¿se comprende mejor ahora?
Entonces: ya tenemos la celda objetivo (la cual SIEMPRE debe contener una función), que es en donde está el gasto total. Ahí le tenemos que decir a Solver que por favor achique lo mas posible ese número, así ahorro plata. Y Solver lo va a reducir, cambiando la cantidad de mercadería enviada a cada ciudad. Entonces, ya tenemos la otra pata: las celdas cambiantes serán las que se encuentran dentro de la segunda tabla. Y ya vimos las restricciones: la producción en cada planta y la capacidad de almacenamiento en cada ciudad.
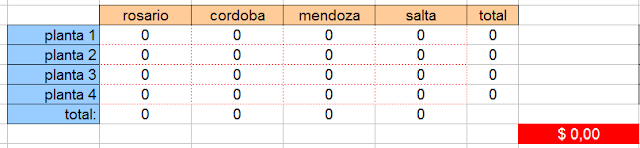
¿Vemos la forma de indicarselo a Solver? Como primer medida, ponemos todos los datos de la tabla inferior en cero, ya que Solver deberá completar esos valores:
todo a fojas cero. la celda objetivo (de rojo) quedó también en cero (recuerden que en su interior está la función =SUMAPRODUCTO(C2:F5;C9:F12) )
Abajo de la tabla colocaré una fila auxiliar, que contendrá el total de almacenamiento de cada ciudad, y a la derecha una columna que nos mostrará la capacidad máxima de producción de cada planta. Lo haré para facilitar la lectura de las restricciones que le daremos a Solver:
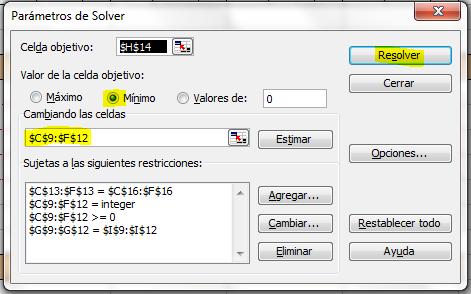
Si leyeron mi entrada previa, ya tienen a Solver instalado. Vamos a Herramientas / Solver y rellenamos el formulario de la siguiente forma:
Rosario puede almacenar hasta 70 memorias, Córdoba 50, etc, etc. Y la planta 1 puede producir hasta 80 memorias, la planta 2 hasta 70, y así hasta el final.
Si leyeron mi entrada previa, ya tienen a Solver instalado. Vamos a Herramientas / Solver y rellenamos el formulario de la siguiente forma:
Analizando:
1) Celda Objetivo: H14 (la que en el ejemplo tengo en rojo). Allí anteriormente habíamos calculado a mano los posibles costos.
2) Valor de la celda objetivo: "mínimo". Aquí le indico que busque el menor valor posible de esa celda. Recuerden que en nuestros intentos obtenimos $256.000 y $250.000... bueno, ahora queremos ver si Solver puede achicar aún mas los gastos.
3) Sujetas a las siguientes restricciones:
1) Celda Objetivo: H14 (la que en el ejemplo tengo en rojo). Allí anteriormente habíamos calculado a mano los posibles costos.
2) Valor de la celda objetivo: "mínimo". Aquí le indico que busque el menor valor posible de esa celda. Recuerden que en nuestros intentos obtenimos $256.000 y $250.000... bueno, ahora queremos ver si Solver puede achicar aún mas los gastos.
3) Sujetas a las siguientes restricciones:
C13:F13=C16:F16: el total a enviar a cada ciudad no podrá ser menor o mayor a su capacidad.
C9:F12=integer: los envíos son enteros. ej: no puedo enviar "media o un cuarto" de memoria.
C9:F12>=0: nunca podría enviar "menos 4 memorias". Solo números positivos
G9:G12=I9:I12: lo producido por cada planta no podrá ser distinto capacidad de trabajo.
Presionamos el botón "Resolver" y nos encontramos con una muy muy grata sorpresa:
Solver nos indica una solución que, comparada con la mejor que obtuvimos "a mano", nos ahorra (lisa y llanamente) la friolera de $95.000. (recuerden que el menor valor fué de $250.000).
Me dijo que debo hacer con cada memoria:
1) desde la planta 1, 39 a Córdoba, 11 a Mendoza y 30 a Salta
2) desde la planta 2, 70 a Salta
3) desde la planta 3, 21 a Rosario y 69 a Mendoza
4) desde la planta 4, 49 a Rosario y 11 a Córdoba
Los cuatro puntos anteriores los resolvió en base a las restricciones que le impusimos: vió la forma mas barata de mandar mercadería a cada ciudad, teniendo como cálculo ambas tablas (costos y cantidad de envíos)
Bueno, habrán visto que esto es maravilloso y les cuento que se aplica mucho en finanzas, ingeniería, aeronaútica y otras cosas por el estilo. Puede ser un poco frustrante al principio "agarrarle la mano" y aprender a plantear correctamente la situación, pero vale la pena.... con creces. Y les digo el por qué: no nos vayamos a intrincados y complejos sistemas aeroespaciales ni de mecánica cuántica, miremos esto: imaginen que tenemos nuestra propia empresa (o bien somos empleados de una) de "delivery" ¿no creen que nos ayudará a mejorar nuestros gastos o ganar buenos puntos frente al jefe, el presentar un trabajo como este? ¿A quién no le gusta maximizar sus beneficios u obtener mejores calificaciones laborales al manejar esta poderosísima herramienta de Excel?
Suerte y aquí les dejo el link al archivo.
C9:F12=integer: los envíos son enteros. ej: no puedo enviar "media o un cuarto" de memoria.
C9:F12>=0: nunca podría enviar "menos 4 memorias". Solo números positivos
G9:G12=I9:I12: lo producido por cada planta no podrá ser distinto capacidad de trabajo.
Presionamos el botón "Resolver" y nos encontramos con una muy muy grata sorpresa:
Me dijo que debo hacer con cada memoria:
1) desde la planta 1, 39 a Córdoba, 11 a Mendoza y 30 a Salta
2) desde la planta 2, 70 a Salta
3) desde la planta 3, 21 a Rosario y 69 a Mendoza
4) desde la planta 4, 49 a Rosario y 11 a Córdoba
Los cuatro puntos anteriores los resolvió en base a las restricciones que le impusimos: vió la forma mas barata de mandar mercadería a cada ciudad, teniendo como cálculo ambas tablas (costos y cantidad de envíos)
Bueno, habrán visto que esto es maravilloso y les cuento que se aplica mucho en finanzas, ingeniería, aeronaútica y otras cosas por el estilo. Puede ser un poco frustrante al principio "agarrarle la mano" y aprender a plantear correctamente la situación, pero vale la pena.... con creces. Y les digo el por qué: no nos vayamos a intrincados y complejos sistemas aeroespaciales ni de mecánica cuántica, miremos esto: imaginen que tenemos nuestra propia empresa (o bien somos empleados de una) de "delivery" ¿no creen que nos ayudará a mejorar nuestros gastos o ganar buenos puntos frente al jefe, el presentar un trabajo como este? ¿A quién no le gusta maximizar sus beneficios u obtener mejores calificaciones laborales al manejar esta poderosísima herramienta de Excel?
Suerte y aquí les dejo el link al archivo.
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones
Etiquetas
Datos
Etiquetas:
Datos
- Obtener enlace
- X
- Correo electrónico
- Otras aplicaciones








Gracias Sid por tu comentario. Si, en realidad Solver es una herramienta muy poderosa, que puede brindar soluciones a problemas de extrema complejidad, en los cuales pueden intervenir una enorme cantidad de variables y restricciones. Por el momento intento brindar ejemplos comunes y "entendibles", por que de lo contrario no se comprende bien y, por ende, descartamos su uso, lo cual es una verdadera lastima.
ResponderEliminarEstoy preparando otro ejemplo con una utilidad poco conocida de Solver, pero muy provechosa para el trabajo.
Un abrazo.