Algoritmos Geneticos en Excel

Volcado, desde hace un par de días, a la resolución de algunos problemas de optimización que me plantearon distintos lectores, decidí levantar la presente entrada, aunque el sistema que utilizaré no será un tema excluyente de Excel. Tampoco resultará algo sencillo para aquellos que nunca oyeron hablar de esta “técnica”, por cuanto habrá que prestar especial atención e ir comprendiendo el “paso a paso”, analizando cuidadosamente todos los proceso que intervienen. ¿Por qué un preludio tan extenso? Por que veremos la forma de realizar Algoritmos Genéticos (Wikipedia), un desarrollo mediante el cual es posible simular en nuestro ordenador el proceso evolutivo de la naturaleza, aplicando sus pasos en la resolución de problemas.

Trataré de evitar a toda costa caer en tecnicismos y funciones por demás de complejas, como intento hacerlo siempre. Material sobre los Algoritmos Genéticos (AG, a partir de ahora) abunda en la Web, pero casi nada de “código resuelto” puede hallarse... por cuanto apuntaré mas a lo práctico que a lo teórico. Es un tema maravilloso y sorprendente, al cual los invito a seguir a lo largo de este extenso post.

Darwin nos enseñó que las especies evolucionan a través de un mecanismo de selección natural, que favorece la supervivencia del mas apto. De esta forma vamos “mejorando” en cada generación, ya que de la población, los mas aptos tienen mayor posibilidad de reproducirse y llevar sus genes “buenos” a la descendencia. Durante el transcurso del Siglo XX a alguien (John Henry Holland) se le ocurrió que un algoritmo podría también evolucionar y “ser mejor”, aplicando las mismas técnicas de la naturaleza: crear una población, seleccionar a los mejores individuos, cruzarlos, mutarlos y así dar paso a una nueva generación, con la ventaja de que esta última nació sobre los cimientos de los mejores genes de la anterior. Y así vamos evolucionando.

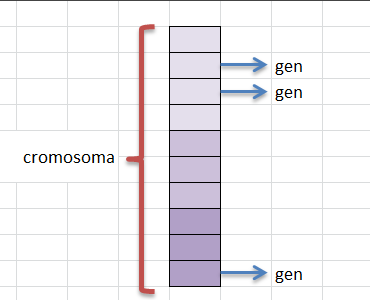
Todo nace a partir del gen, considerado como la unidad de almacenamiento de información genética. Allí “ya está escrito” que color de ojos tendremos, nuestra altura, enfermedades, etc, etc, etc. Un cromosoma es, a grandes rasgos y hablando en términos generales, una “ristra” de genes. Veamos como luce un cromosoma "armado en Excel"

ahá, así de sencillo, por ahora. Un cromosoma no es mas que una matriz, donde cada elemento es denominado gen y almacenará información sobre nuestro problema. El cromosoma del ejemplo posee 10 genes

Reduciendo las cosas a la mínima expresión (y repito, obviando cualquier tecnicismo), yo estoy escribiendo esto luego de que los cromosomas de mi mamá se cruzaron con los de mi papá, heredando genes de unos y otros. Y a Ud. que están leyendo esto... les pasó los mismo. En medio de ese “cruzamiento” se produjo alguna que otra mutación genética, principio fundamental para asegurar la diversidad. De esta forma se generan las poblaciones y, según lo expuesto por Darwin y ya recontra probado, cada generación “avanza” con respecto a la otra, proporcionando individuos mas aptos.

una clásica reproducción sexual de los cromosomas (crossover): cromosoma papá a la izquierda, cromosoma mamá a la derecha y en el medio, el nuevo cromosoma, el cual hereda genes de sus padres. Noten, para ir entrando en calor, que el último gen no es ni azulado o rosa: es verde... allí se produjo una mutación.

Si todo salió bien ese gen "Yo" es mejor que los genes "Papá" y "Mamá", y a su vez contribuiré a la creación de una población mas evolucionada, dado que (si todo sale bien) me cruzaré con otro cromosoma que pasó por la misma experiencia.

Ahora intentemos llevar toda esta parafernalia evolutiva a nuestra especialidad.

Los AG se utilizan en la resolución de problemas que involucran muchas variables y restricciones, en donde existe una gran cantidad de elementos a combinar. Por ejemplo, son utilizados para los sistema satelitales de los GPS, calculando la ruta entre X cantidad de puntos. Jaja, si, parece mentira, pero una de sus funciones puede ser esa. Brindo ese ejemplo para que se comprenda la complejidad de resolver el mismo caso mediante la “fuerza bruta”: imaginen probar todas las combinaciones posibles de todas las ciudades de un país para calcular la ruta mas corta. Serían trillones y trillones de alternativas a evaluar... así que para cuando el GPS nos de la solución, probablemente la ruta o ciudad no existan mas. Así de sencillo.

Empecemos. ¿Cómo trabaja un Algoritmo Genético? Primero vamos a un ejemplo "en blanco", similar a las imágenes ya mostradas. Nuestro AG debe:

1) Generar una población de cromosomas: esto se realiza de forma aleatoria, al igual que en la naturaleza.

creamos 6 cromosomas (los colores son solo para ilustrar)

noten que ya empezamos: cada gen tiene un valor: 1 ó 0 , que es la forma mas habitual de codificar un AG.

nuestros cromosomas contienen información, y sobre ella trabajaremos

Cada 1 / 0 que se observa fué colocado de forma aleatoria: como tirar una moneda al aire, si sale "cara" coloco un 1, si sale cruz, un 0.

2) Seleccionar los mas aptos: aplicando una función de ajuste (fitness) que evalúe los 6 cromosomas y, por ejemplo, seleccione a los dos mejor dotados, es decir, los mas aptos para reproducirse. Ej: nuestra macro, por sí sola, no puede decir cuales de esos 6 cromosomas son "los mejores"; ahí es donde debemos crear una "función de ajuste" que los analice y sobre la base de nuestras premisas, sepa seleccionarlos. Supongamos, por ahora, que los mejores cromosomas son aquellos que poseen mas genes codificados con 1. Entonces:

de acuerdo a nuestro "fitness"  el primer, segundo y sexto cromosoma son los mas aptos, ya que contienen mas cantidad genes con valores iguales a 1.

3) Cruzamiento (crossover): aquí se inicia la reproducción sexual de los dos mejores cromosomas. Tomemos el primero y segundo, los cruzamos y vemos como nos queda el hijo. Existen muchísimas formas de realizar el crossover, pero no me explayaré sobre las mismas por que si no esta entrada sería por demás de extensa. Voy a elegir (tambien de forma aleatoria) dos números entre 1 y 10, es decir, la cantidad total de genes de cada cromosoma. Supongamos que salieron el 4 y el 8, a los cuales llamaremos "puntos de cruce" y será la porción del cromosoma que herede genes de los dos padre seleccionados. Observen la siguiente imagen (quité tantos colores para evitar confusiones):

esta es nuestra población original. Conservan los genes 1, 2, 3, 9 y 10. Los genes 4,5,6,7 y 8 serán completados con información de sus padres.

Y este pase de genes también será aleatorio: vamos a recorrer cromosoma x cromosoma (los 6 de la población actual) y cada vez que nos hallemos entre el gen 4 y el 8 lanzaremos la moneda: si sale cara, hereda de un padre, si sale cruz, hereda del otro. No es nada mas ni nada menos que un bucle recorriendo una matriz. Hice todo a mano (ya veremos la codificación), obteniendo el siguiente resultado:

Bien, arriba tenemos a la nueva generación, luego de haber combinado los genes de los dos mejores cromosomas seleccionados. Parece todo igual, pero no es así: la suma de todos los 1 de la primer generación arroja un total de 30.... en esta segunda generación 33. Es decir, claramente, que nuestra población evolucionó hacia sujetos con mas genes codificados con 1, que es lo que requerimos en nuestra "función de ajuste" Y si repito la operación, me voy a 38 y luego a 45 y así sucesivamente, hasta encontrar un valor óptimo. ¿Se entendieron los pasos y observaron como en realidad esos cromosomas evolucionaron hacia una respuesta mejor?

Bueno, para alegría de todos, ese mecanismo se emplea en resolver problemas financieros, de física, de logística, biología,  inversiones y de casi todo lo que se les pueda imaginar.
Para ir cerrando la teoría: los AG en si mismo son todo un universo aparte, del cual podrán encontrar mucha información en la web. Para cada una de las cosas que detallé existen cientos de formas de hacerlas distintas y esas formas dependerán en gran medida de las características de nuestro proyecto. Aquí trato de exponer lo básico y fundamental:
1) generamos una población de cromosomas, en donde cada uno de ellos es una posible solución a nuestro problema. Cabe destacar que se hace aleatoriamente: cada gen del cromosoma tomará un valor al azar, obviamente, dentro del rango de valores que ocupa nuestro problema a resolver (en el ejemplo de arriba, unos y ceros)
2) seleccionamos los mejores individuos, en base a una función "de ajuste" (fitness) que evalúa cual de ellos cumple con las condiciones ideales. Esta función puede ser algo tan sencillo como una suma o una resta, o bien poseer complicados mecanismos de evaluación (depende del proyecto)
3) sobre la base de los genes de los cromosomas seleccionados en el paso anterior mejoramos la población, en la fase denominada reproducción sexual o combinación (crossover), definiendo, tambien al azar, los "puntos de cruce" es decir, a partir de "donde" y "hasta" que genes se intercambiarán. Aquí se produce también (al azar y en porcentajes muy bajos) la "mutación", indispensable para que exista la diversidad. Ampliaré este concepto en la codificación del AG.
4) volvemos sobre el punto 2 y 3, hasta encontrar una solución óptima.

A medida que vayamos desarrollando el código iré explicando otras cosas que aquí se me complica hacerlo, aunque "la base está" y ya tenemos todo listo para empezar.
¿Cuantas generaciones hacen falta para llegar a nuestro "cromosoma ideal", o sea, nuestra solución? No se sabe, por ello es conveniente ir "guardando" los resultados para un posterior análisis.
Larguemos.

¿Han oído hablar del "Problema de la Mochila"? Este nos plantea lo siguiente: " existe una mochila con, por ejemplo, una capacidad máxima de 20 kg de carga. A esa mochila debemos llenarla con distintos objetos (imaginemos que nos vamos de campamento) los cuales tienen un peso y una utilidad determinada. ¿Cual es la forma óptima de cargar esa mochila? ¿Que combinación de elementos me dará el máximo beneficio (utilidad) sin pasarme de los 20 kg máximos permitidos?"
Como podrán ir imaginando pueden existir cientos de miles de combinaciones distintas, de acuerdo a la cantidad de objetos existentes. Si bien el Problema de la Mochila es válido en si mismo, les aclaro que estamos ante algo "teórico", dado que en realidad ese tipo de planteamientos es utilizado, por ejemplo, en situaciones como fabrico camisas, pantalones y remeras, las cuales me representan un costo ("peso" en la mochila) de $10, 15 y 8, con una utilidad ("beneficio" en la mochila) de $3, 4, y 5 respectivamente. Si tengo 2600 mts de tela ¿cuantas unidades de cada artículo me conviene producir para obtener el máximo beneficio?
A ese tipo de problemas apunta en forma teórica nuestra Mochila, pero nos quedaremos con ella, para hacer mas fácil la comprensión y aplicación de los AG. Como digo siempre: para complicarla, sobra tiempo.

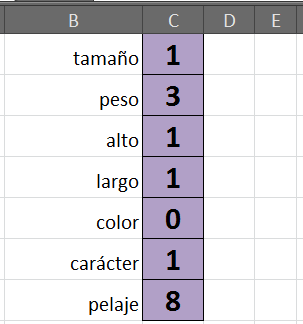
Nuestra mochila es sencilla y contendrá elementos básicos para irnos de campamento. Los valores utilizados son irreales y con fines meramente descriptivos, pero nos permitirán apreciar el peso de cada uno (que pueden ser expresados en kilos y cualquier otra unidad) y un beneficio:

nuestra querida mochila. Como vemos, no podemos incluir todos los elementos, ya que totalizan un peso total de 27, y esta tiene una capacidad máxima de 20.

Para no ir perdiendo "la pisada" y "enganchar" con la teoría repasada hasta el momento, les mostraré la misma tabla, pero a la derecha observarán tres "cromosomas" (posibles soluciones) al problema:

Codifiqué de forma binaria el problema y ahí tiene 3 cromosomas: cada gen posee un 1 o un 0, que significan: incluyo el objeto (1) ó no lo incluyo (0).
Antes de seguir, analicemos esos 3 individuos: veamos que peso y utilidad tienen cada uno de ellos:

Para que se entienda: multiplico cada gen del cromosoma por el peso del objeto, si es 1 me devuelve el peso y si es 0.... queda en 0. Luego sumo los resultados de esas multiplicaciones. Y luego hago lo propio con la utilidad. Para ambas apliqué =SUMAPRODUCTO(matriz1, matriz2).
Ya tenemos un panorama mucho mas claro: el primer y segundo cromosoma no pasan nuestra prueba, ya que exceden los 20 kg que soporta la mochila. El tercero es el apto y nos servirá para mejorar la población e ir arrimándonos a la solución mas óptima ¿Se va entendiendo la lógica?

Lo arriba desarrollado nos permite inferir cual será nuestra "función de ajuste" (fitness) y así indicarle a nuestra macro que cromosoma "sirve" y cual no. Lo principal será evaluar que la suma de los pesos de los objetos no superen los 20 kg y, a su vez, tengan la utilidad o beneficio mas alta. Podrán ir imaginando también que existirán varias soluciones posibles: luego determinaremos si dejamos la elección final a un criterio mas "humano" o desarrollamos algún código que seleccione la mejor.

Pasemos a un rudimentario pseudocódigo:
Procedimiento AlgoritmosGeneticos()
generar una poblacion de 10 cromosomas, asignando de forma aleatoria a cada gen un 1 o un 0
repetir
  seleccionar los 2 mejores cromosomas, en base a nuestro "fitness" (función de ajuste)
  cruzar los 2 cromosomas con la población, generando una nueva
fin repetir
Fin Procedimiento

Aprovecharemos las bondades de Excel, haciendo uso de sus rangos y ahí crear los cromosomas, tal como lo fui mostrando hasta el momento. En una hoja aparte iré guardando los cromosomas "padres", es decir, los mejores, así tenemos un historial de las mejores selecciones y posteriormente decidir con cual de ellas nos quedamos No olvidemos que las combinaciones posibles son muchas y si nos ajustamos estrictamente al problema de la mochila... quizás para algunas será mas conveniente llevar mantas o para otros reemplazar dicho objeto por una linterna, siempre y cuando no supere los 20 kgs de capacidad.

Lo que visualizan en la imagen superior lo realicé para facilitar las cosas. Diseñé el "esqueleto" de los 10 cromosomas que se formarán en cada generación y desde el cuadro de nombres (arriba a la izquierda) los nombré, para luego identificarlos desde VBA (cromosoma_1, cromosoma_2..... cromosoma_10).
Si no estamos en Excel, o bien no queremos hacer uso de rangos o el tamaño de la población necesite ser mas flexible, todo esto se reemplaza por una común y corriente matriz bidimensional:
Dim Población (1 to 10, 1 to 10) as Variant

En lo personal siempre agrego un par de "genes" a cada cromosoma, para guardar información adicional sobre el individuo. De esta forma sé que las soluciones llegan al gen nro 10, pero a partir de allí almaceno datos sobre distintos aspectos de ese cromosoma en particular. Me resulta imprescindible en proyectos de mayor complejidad, como seguramente alcanzarán a realizar luego de descubrir esta increíble forma de trabajo.
Generemos la primer población, de 10 cromosomas y asignemos a cada gen, de forma aleatoria, un valor (entre 1 y 0, para este caso):

Bien, ya tenemos a cada individuo (cromosoma) de la población con sus genes completos:

Ahora viene un tema delicado: el "fitness", ya que debemos seleccionar a los dos mejores individuos de la población, aspecto que será decisivo para llegar a buen puerto. Por un lado es fácil: solo serán aptos aquellos cuyo peso no supere los 20 kgs de nuestra mochila: los cromosomas 2, 3 y 6 quedan descartados de la selección. Pero por el otro lado.... ¿cual es mejor, el primero con un peso muy liviano de 11 y una utilidad muy alta de 19, o el décimo, con mucho peso y alta utilidad? Yo diría que el primero, ya que me permitirá seguir agregando elementos a la mochila y así ir incrementando la utilidad total.
Mi "función de ajuste" es la que se observa en la fila correspondiente a "puntuación" y utilizo a las funciones =SI() y COINCIDIR() para lograrla. En el libro que les dejo al pié del post podrán analizarla, pero en principio les aclaro:
1) primero solo tengo en cuenta los cromosomas de peso <= 20
2) luego me fijo cual es la utilidad mas alta de dichos cromosomas
3) sumo el resultado del punto 1 + el resultado del punto 2, obteniendo una "puntuación"... mientras mas alta, mas apto el individuo y con mas posibilidades de ser elegido como padre.

según mi función de ajuste, los mas aptos son el primer y cuarto cromosoma, ya que con poco peso reportan una utilidad alta.

¿Pueden ver ahora lo que les quería decir con "agregar genes para almacenar información"? Bien podría ahora extender la cantidad de genes a 13 y guardar en los ultimos 3 el peso, la utilidad y la puntuación. Por que ahora la cosas se simplifican al utilizar rangos de Excel, pero de lo contrario debería ser mas cuidadoso con el armado de las matrices. Pero bueno, lo veremos en futuras entradas, hoy el tema es aprender a manejar los AG. Sigamos.
En la última fila (fila nro 15) tengo las puntuaciones, las recorro con un bucle y selecciono las dos mejores, que pasarán a ser los futuros "padres" de la siguiente generación.
Con este código recorro toda la población de cromosomas y elijo a los dos mejores, en base al fitness:

Sub SeleccionarPadres()
Dim X, C As Byte
Dim Cromosoma, CromoPadre1, CromoPadre2 As Range
Dim Optimo, Optimo2

Optimo = 0
Optimo2 = 0
'recorro todos los cromosomas, para identificar en que columna
'de la planilla están cada uno de ellos:
For X = 1 To 10
    Set Cromosoma = Range("cromosoma_" & X)
    'tomo la columna
    C = Cromosoma.Column
    'si el peso es menor o igual a 20
    If Cells(13, C).Value <= 20 Then
        'guardo el fitness del mas apto
        If Cells(15, C).Value > Optimo Then
            Optimo = Cells(15, C).Value
            Set CromoPadre1 = Cromosoma
        End If
    End If
Next X
'copio el cromosoma padre 1 en un rango, para dejarlo
'guardado y usarlo en el cruzamiento:
CromoPadre1.Copy Range("padre_1")

'ahora voy por el segundo padre. es igual a lo anterior,
'salvo que Optimo2 debe ser menor a Optimo, por que ahora
'hablamos del segundo padre:
For X = 1 To 10
    Set Cromosoma = Range("cromosoma_" & X)
    C = Cromosoma.Column
    If Cells(13, C) < 20 And Cells(15, C) < Optimo Then
        If Cells(15, C) > Optimo2 Then
            Optimo2 = Cells(15, C)
            Set CromoPadre2 = Cromosoma
        End If
    End If
Next X
'guardo el segundo padre:
CromoPadre2.Copy Range("padre_2")

'llevo ambos padres a un backup, para ir viendo los
'mejores de cada generacion
With Sheets("mejores")
fila = .Cells(Cells.Rows.Count, 1).End(xlUp).Row + 2
CromoPadre1.Copy .Range("a" & fila)
CromoPadre2.Copy .Range("c" & fila)
'coloco los totales
Range("tot_padre_1").Copy
.Range("a" & (fila + 10)).PasteSpecial xlPasteValues
Range("tot_padre_2").Copy
.Range("c" & (fila + 10)).PasteSpecial xlPasteValues
'coloco los nombres de los objetos seleccionados
For X = fila To (fila + 9)
    i = i + 1
    If .Range("a" & X) = 1 Then
        .Range("b" & X) = Range("objetos").Cells(i)
    End If
    If .Range("c" & X) = 1 Then
        .Range("d" & X) = Range("objetos").Cells(i)
    End If
Next X
End With

'destruyo los objetos:
Set CromoPadre1 = Nothing
Set CromoPadre2 = Nothing
Set Cromosoma = Nothing
End Sub

Logrando esto:

la macro recorrio y, a la derecha, coloco los dos mejores... los mas aptos para reproducirse.

Sobre la base de lo mencionado hasta el momento, el código para cruzar la población actual con los padres es el siguiente:

Sub Cruzamiento()
Dim Desde, Hasta, X, Muta, J As Byte
Dim Cromosoma As Range

Randomize
'gen de inicio
Desde = CByte(Application.WorksheetFunction.RandBetween(1, 9))
'gen de fin
Hasta = CByte(Application.WorksheetFunction.RandBetween(Desde, 10))

'recorro los cromosomas
For X = 1 To 10
    Set Cromosoma = Range("cromosoma_" & X)
    'intercambio los genes de los padres con los genes
    'de los cromosomas, entre los puntos aleatorios:
    For J = Desde To Hasta
        'si sale 1 pongo el gen del padre1, si sale 0
        'pongo el gen del padre2
        If CByte((1) * Rnd) = 1 Then
           Cromosoma.Cells(J) = Range("padre_1").Cells(J)
        Else
           Cromosoma.Cells(J) = Range("padre_2").Cells(J)
        End If
        'y la mutación (la explico mas abajo). si el gen
        'tiene valor 1 le pongo 0, si tiene 0, le pongo 1
       
        'primero  genero un valor aleatorio, entre 1 y 100
        Z = Application.WorksheetFunction.RandBetween(1, 100)
        'y le doy un 1% de probabilidad. si se cumple, hay
        'mutación:
        If CByte(Z) = 50 Then
            If Cromosoma.Cells(J) = 1 Then
                Cromosoma.Cells(J) = 0
            Else
                Cromosoma.Cells(J) = 1
            End If
        End If
    Next J
Next X

Set Cromosoma = Nothing
End Sub

Como habrán visto todo es bastante aleatorio, tal cual los postulados de nuestra madre naturaleza.
Notarán que generé un número al azar, entre 1 y 100... si ese número es igual a 50, cambio el valor de uno de los genes, deliberadamente. ¿Por que hago eso? Allí estamos frente a la indispensable mutación, que nos asegura una sola cosa: diversidad. Si no existiera un factor de mutación (del 1% en este caso, que generalmente es lo aconsejable) nuestra población tendería a igualarse, sin generar soluciones nuevas.
Factores de mutación muy altos también nos perjudicarían, dado que crearíamos nuevos "seres", totalmente distintos a sus padres y población original. ¿Se comprende?
Un ejemplo bien práctico: mis padres se reprodujeron, yo soy la combinación de sus genes. Existió una mutación que dio origen a un nuevo ser (el que ahora escribe esto), igual a sus padres... pero distinto, por que ciertos genes cambiaron (mutaron) en el proceso. Pero (y aunque la mayoría de mis amigos no este de acuerdo) mutaron dentro de parámetros normales, ya que caso contrario tendría 3 piernas, 4 brazos o mi cabeza sería de color verde con cerdas amarillas. "Mucha mutación" habría generado un nuevo ser, hasta quizás de otra especie, que nos alejaría del concepto de ser humano que tenemos. Bien... con los AG sucede exactamente lo mismo. Factores de mutación muy altos nos generarían cromosomas que no estarían acordes a la "población" de soluciones. Y muy bajos harían que padres e hijos sean totalmente iguales, homogeneizando la población ("convergiendo", en nuestra jerga), estandarizando así las soluciones y no proponiendo nada nuevo.

Y ahora... a los bifes se ha dicho. Agregué cierto código que va guardando en otra hoja los "mejores padres", así con posterioridad los analizamos, junto a una celda que me va diciendo cuantas generaciones tengo realizadas.
Veamos en imágenes que sucede:
1) Genero la población aleatoria:

a la derecha los mejores cromosomas de la población: 19 de peso con 26 de utilidad (cromosoma nro 10) y 17 de peso con 21 de utilidad (cromosoma nro 3)

Presiono el botón para cruzar los "padres" con la población y obtengo esto:

Bingooooo!!! quiero decir... ciencia. Ya tenemos una solución factible: el cuarto cromosoma, alcanzó el peso de 20 con una utilidad de 23.

Sigamos creando generaciones de cromosomas e intercambiando sus genes con los mejores padres:

en la séptima generación el primer padre sigue igual, pero el segundo "saltó" a un peso de 19 y utilidad de 21. Bien, vamos evolucionando.

Y seguimos. La generación 23 me trae esto:

bajamos un poco el peso y subimos las utilidades por mochila

Y en la generación 67:

esooooo !!!!! una mochila de peso 20 con utilidad de 27. Jeje, mis pequeños han evolucionado de forma excelente.

La macro se encargará de hacer esto:

nos irá guardando el historial de los "mejores padres", para que al final sepamos como combinar los objetos dentro de la mochila, junto al peso, utilidad y puntuación obtenidas por los padres en cuestión.

Abren el libro, presionan "generar poblacion", luego "seleccionar padres" y finalmente "cruzar cromosomas". Los botones se irán ocultando/mostrando para guiarlos, ya que como habrán visto podemos llegar a necesitar varios "bucles" hasta llegar a una de las posibles soluciones. Quizás lo ideal sería colocar todo dentro de un bucle, pero lo dejo así por que cada vez que presionen un botón tendrán la posibilidad de ir viendo como evolucionan los padres, y es bastante interesante observarlo en "camara lenta".

Como ya mencioné, existen cientos de formas de selección y cruzamiento (por ponderación, totalmente aleatoria, de la ruleta sesgada, etc, etc, etc, etc), pero mi intención no es embrollar las cosas. Nunca pude encontrar el código en VBA de un algoritmo genético, por cuanto ese fue mi objetivo: mostrar en forma práctica (y lo mas sencillamente posible) como se programa un AG y para que se utiliza.
Recuerden que "La Mochila" puede ser una empresa, mientras que los objetos la producción, junto a sus costes y beneficios individuales... y de esta forma sabremos que y como fabricarlo.
Prueben cambiando los pesos y utilidades de los objetos de la mochila, o bien asignando un factor de mutación mas alto.... verán como las cosas cambian; es un buen ejercicio para saber lo importante que se tornan el correcto manejo de las variables en juego.

Otra cosa mas, antes de despedirme. A cada cromosoma lo codifiqué con números binarios, que por lo general es la forma mas habitual de hacerlo. Pero podemos ir mucho mas allá, y les tiro la idea para que la piensen y analicen, saliendo un poco de los 1 y 0.
Supongamos que tenemos un criadero de perros, dedicándonos a la cruza de distintas razas. ¿Como codificaríamos el cromosoma de un perro? Aquí va una:

Si: cada gen de ese cromosoma (perro) es una característica: pelaje, color, altura, etc, etc, etc. Los valores utilizados para el ejemplo son referenciales y, obviamente, deberán guardar relación con una tabla lógica que tengamos armada. Podríamos decir que este es un caniche:

Chico, con mucho pelo, buen caracter, blanco (color=0), liviano.... si, casi un "excel_caniche".
Y este un Gran Danes:

Entonces ¿que nos priva de generar diez perros (cromosomas) con valores aleatorios y luego combinarlos, hasta encontrar "el perro ideal" (gris, mediano, de caracter agresivo, etc, etc) para saber como cruzarlos? Nada, no tenemos nada de privativo en esto, y sería un buen ejercicio para ir entrando en el mundo de los AG. Y este tipo de trabajos es válido para realizar proyecciones empresariales, científicas o casi de cualquier índole. Espero que les sea de utilidad.
Un abrazo y Link al archivo.